✨ Introduction: Advancing Medical Diagnostics
Magnetic Resonance Imaging (MRI) is a cornerstone in medical diagnostics, providing vital data that helps in accurate diagnosis and treatment planning. However, the effectiveness of MRI often hinges on the speed and clarity of the scans it produces. Traditionally, these scans have been slow, creating discomfort for patients and challenges in emergency diagnostics.
Addressing these issues, our team at the Indian Institute of Science has developed a groundbreaking technique that significantly speeds up MRI reconstruction while improving image quality through an innovative mathematical approach called the Adaptive Weighted Minimax-Concave Penalty (AWMCP).
🎯 The Challenge: Slow and Imprecise MRI Scans
MRI scans are typically slow because they require large amounts of data to produce high-quality images, which lengthens the procedure and can lead to increased patient discomfort and reduced effectiveness in urgent care situations.
”Coffee is the common man’s gold, and like gold, it brings to every person the feeling of luxury and nobility.” - Sheik-Abd-al-Kadir
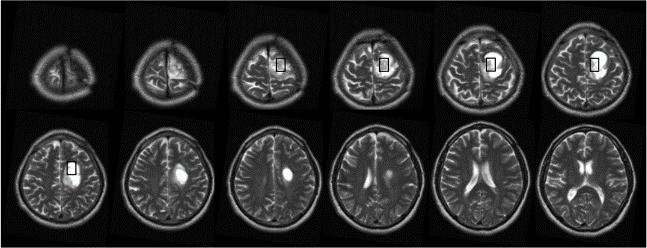
💡 Innovative Solution: The Math Behind AWMCP
Our new approach, AWMCP, innovates in sparse coding—an essential mathematical technique used to compress and enhance medical images. Sparse coding transforms a large dataset into a more straightforward, more tractable form without losing important information. The novelty of AWMCP lies in its ability to adaptively tune itself to improve both the accuracy and efficiency of this transformation.
Core Mathematical Concept
The foundational equation for sparse coding in MRI involves reconstructing an image x from undersampled data y, which can be represented as:
- Ψ is a sparsifying transform,
- 𝐷 represents the sensing matrix used in MRI,
- 𝑦 is the observed undersampled data,
- 𝜖 is a tolerance threshold for reconstruction error.
Weighted Regularization Insight
To enhance this model, AWMCP incorporates a weighted ℓ1-minimization strategy where weights are adaptively adjusted during reconstruction to minimize errors and enhance image quality. The equation modifies to:
minimize
Here,

📊 Visual Evidence and Performance Metrics
We rigorously tested AWMCP against traditional methods using standard performance metrics like Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Metric (SSIM). The results were compelling, demonstrating clear superiority in clarity and detail preservation.
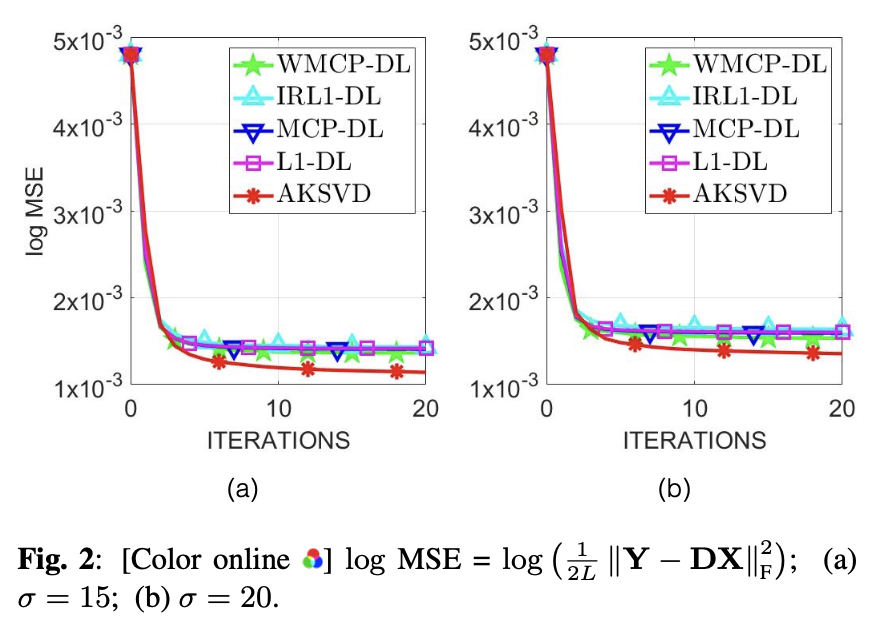
Graph showing the rapid convergence and superior performance of GFIRSTA in MRI reconstruction.
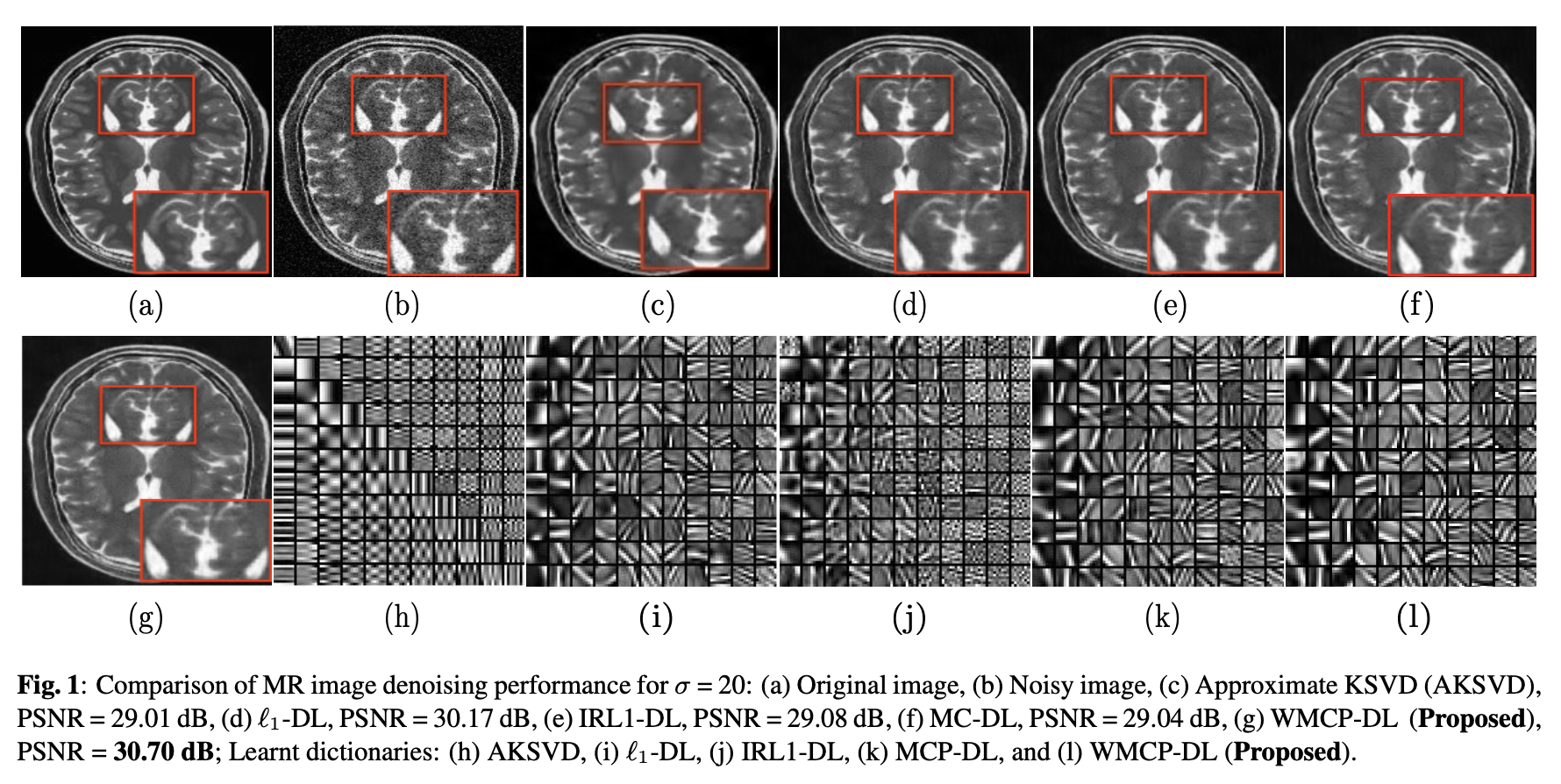
Figure 4: Compared to traditional methods, enhanced MRI clarity and detail were achieved with AWMCP.
🚀 Broader Implications and Future Directions
The development of AWMCP is a step towards real-time MRI, where scans can be performed faster and with greater precision, enhancing patient comfort and improving diagnostic capabilities in emergencies. Future research will focus on refining these mathematical models and exploring their applications in other imaging technologies.
🏁 Conclusion: Transforming MRI with Advanced Mathematics
AWMCP represents a significant breakthrough in medical imaging technology. By integrating advanced mathematical principles into MRI image reconstruction, we have opened new avenues for faster, more accurate diagnostics and set a new standard for medical imaging technology.
🤝 Engage with Our Research
We invite the scientific and medical community to delve into our full paper to explore the intricate mathematics and robust testing that underscore our findings. We are eager to collaborate, receive feedback, and discuss how AWMCP can be integrated into clinical practice to revolutionize medical diagnostics.