Phase Estimation in Imaging Technology

Phase estimation is integral to various advanced imaging technologies, from satellite imagery to medical diagnostics. However, extracting accurate phase information from noisy data remains a challenge. Our team at the Indian Institute of Science has pioneered a novel approach that significantly refines this process. We introduce the Improved Sparse Interferometric Phase Estimation (iSpInPhase) method, employing non-convex optimization to achieve remarkable improvements in accuracy and efficiency.

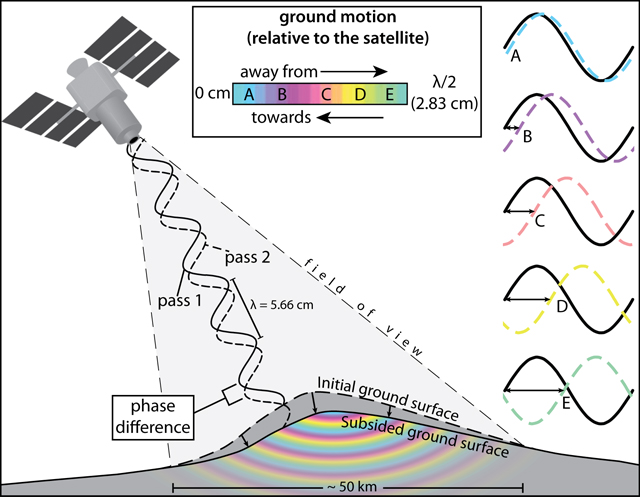Fig.: InSAR Technology

Accurate phase estimation is crucial in applications like interferometric synthetic aperture radar (InSAR) and medical imaging, where detailed and precise imaging is required. Traditional methods need help with noise and data incompleteness, often resulting in distorted images that can lead to inaccurate conclusions.

”In our rush to the future, we often forget the beauty of the past.” - Yours Truly

Our approach, iSpInPhase, incorporates the minimax concave penalty (MCP) and the smoothly clipped absolute deviation (SCAD) penalty, customized for complex-valued data. These advanced mathematical strategies allow us to handle non-holomorphic functions effectively, a common challenge with complex data in imaging technologies.

iSpInPhase revolutionizes how we estimate phase using non-convex regularizers, providing greater flexibility than traditional methods. We utilize the Alternating Direction Method of Multipliers (ADMM) and Wirtinger calculus to solve the optimization problems efficiently and accurately.

1. Complex-Domain Sparse Coding and Dictionary Learning

   • Problem Statement: Traditional sparse coding methods are not efficient for complex-domain data which is common in SAR imaging due to the phase and amplitude information.

   • Innovative Solution: We extended the Sparse Coding framework to the complex domain using non-convex penalties, which better handle the irregularities and discontinuities present in SAR data.

   • Mathematical Model

     min $\frac{1}{2}\mathrm{\Vert <!--Integral\; -->}y-\mathrm{Dx}{\Vert <!--Integral\; -->}_0^1+P(u)\text{s.t.}u=x,\Vert d_{\mathrm{i}}{\Vert }_2^2=1,\forall i$

     Here, 𝑦 is the observed data, 𝐷 is the dictionary representing the basis functions, and 𝑥 is the sparse coefficient matrix in the complex domain. 𝑃(𝑥) represents the non-convex penalty function applied to promote sparsity.

   • Technique Used: ADMM for alternating minimization combined with Wirtinger calculus for handling the complex data structures.

2. Proximal Operators for Non-Convex Regularization:

   • Functionality: These operators enable the handling of sparsity in the phase data more effectively, improving the quality of the reconstructed images.

     • Technique Applied: We adopted two specific non-convex penalties: the Minimax Concave Penalty (MCP) and the Smoothly Clipped Absolute Deviation (SCAD), both extended to handle complex data.

   • Advantage: These penalties are particularly effective in reducing the bias that standard 𝐿₁ penalties introduce in high-dimensional data, thus maintaining the integrity of significant signals while suppressing noise.

   • Mathematical Formulation:

     $\mathrm{MCP}:\lambda \mathrm{|x|}-\frac{{\mathrm{|x|}}^2}{2\gamma }for\mathrm{|x|}\le \mathrm{\gamma \lambda }$

     This formula shows how MCP is applied to each coefficient, reducing the penalty progressively as the coefficient value increases, thereby allowing more significant coefficients to be preserved.

Integration of Wirtinger Calculus

• Purpose: The Wirtinger calculus is crucial for handling functions of complex variables where traditional differential calculus does not apply.

• Application in iSpInPhase: It facilitates the derivation of gradients and integration within the ADMM framework, allowing for efficient optimization in complex-valued data scenarios.

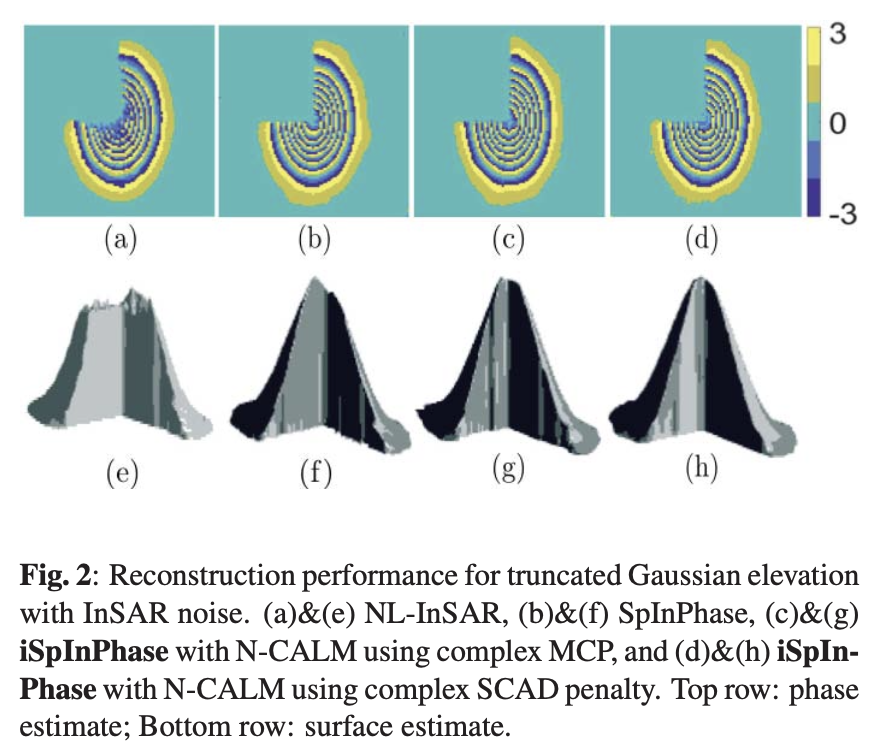
Our tests demonstrate that iSpInPhase outperforms existing state-of-the-art methods significantly. Using synthetic data and real-world scenarios, such as Long’s Peak mountain terrain, we observed substantial improvements in image clarity and detail.

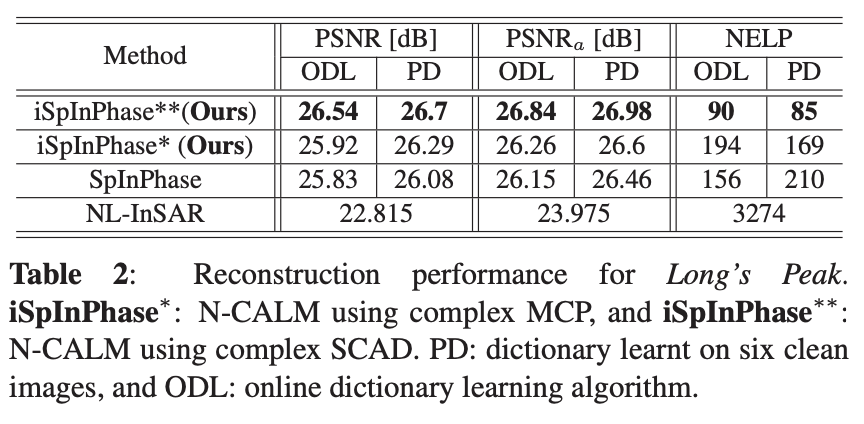
The table showing Peak Signal-to-Noise Ratio (PSNR) comparisons.

Before-and-after images of phase reconstruction showcasing the clarity achieved with iSpInPhase.

The success of iSpInPhase has potential applications beyond traditional imaging, including geological studies, environmental monitoring, and medical diagnostics. This method’s adaptability could redefine standard practices in fields that rely on precise imaging.

The iSpInPhase algorithm sets a new benchmark in phase estimation technology. By integrating sophisticated mathematical techniques, we enhance the fidelity and speed of imaging, paving the way for advancements across various scientific domains.

We encourage the academic and professional communities to delve deeper into our findings. Your insights and discussions are invaluable as we continue to refine this technology. Please access our full research paper for a detailed exploration of our methodologies and comprehensive results.

Read the Full Paper 📝